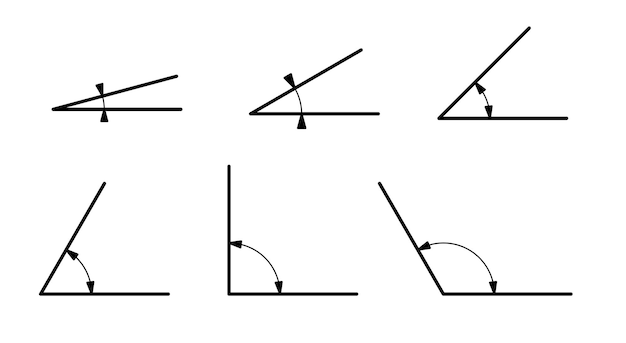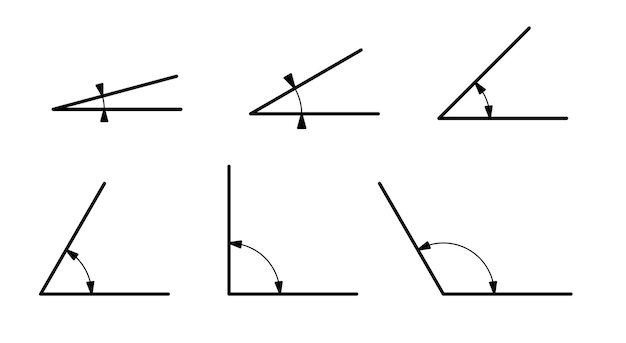
Contents
- 1 Introduction
- 2 Skill #1: Identifying Angle Types
- 3 Skill #2: The Parallel Lines Theorem
- 4 Skill #3: Angle Relationships with Transversals
- 5 Applications in Real Life
- 6 Practical Tips for Mastering Angles and Parallel Lines
- 7 Practice Makes Perfect: Solving Problems
- 8 Conclusion: Your Path to Geometry Mastery
- 9 FAQs
Introduction
Before diving into the specific skills, let’s understand why angles and parallel lines are significant. These concepts form the foundation of geometry, serving as building blocks for more advanced mathematical principles and real-world applications. Whether you’re designing a bridge, creating computer graphics, or simply trying to calculate distances, angles and parallel lines are indispensable tools.
Skill #1: Identifying Angle Types
Acute Angles
Acute angles are the ones that measure less than 90 degrees. They often appear in shapes like triangles and squares, adding sharpness and precision to geometric figures.
Obtuse Angles
Obtuse angles measure more than 90 degrees but less than 180 degrees. Recognizing these angles is crucial when dealing with various polygons and complex shapes.
Right Angles
Right angles measure exactly 90 degrees and are frequently encountered in everyday objects, like the corners of a book or the edges of a square.
Straight Angles
Straight angles are the largest possible angles, measuring 180 degrees. They are the essence of a straight line and play a vital role in understanding parallel lines.
Skill #2: The Parallel Lines Theorem
Parallel lines are lines that never intersect, and they introduce a plethora of geometric possibilities. The parallel lines theorem states that when a pair of parallel lines is intersected by a transversal line, specific angle relationships emerge. These relationships include corresponding angles, alternate interior angles, alternate exterior angles, and consecutive interior angles.
Skill #3: Angle Relationships with Transversals
Corresponding Angles
Corresponding angles are located at the same positions on the intersected lines, and they are congruent, meaning they have the same measure.
Alternate Interior Angles
Alternate interior angles are found on opposite sides of the transversal line and are also congruent.
Alternate Exterior Angles
Just like alternate interior angles, alternate exterior angles are congruent and located on opposite sides of the transversal line.
Consecutive Interior Angles
Consecutive interior angles are supplementary, meaning the sum of their measures is 180 degrees. They are also known as same-side interior angles.
Applications in Real Life
Understanding angles and parallel lines extends beyond the classroom. Architects use these concepts to design structures, ensuring stability and aesthetics. Engineers employ them to construct roads, bridges, and electrical circuits efficiently. Even artists use geometry to create perspective in paintings and sculptures.
Practical Tips for Mastering Angles and Parallel Lines
- Practice regularly: Geometry is a skill that improves with practice. Solve problems, work on exercises, and apply what you’ve learned.
- Visualize: Use diagrams and drawings to visualize angle relationships and parallel lines.
- Seek help when needed: Don’t hesitate to ask teachers, peers, or online resources for assistance.
- Real-world examples: Apply geometry to real-life situations, making it more relatable and memorable.
Practice Makes Perfect: Solving Problems
Now that you’ve grasped the fundamental skills of angles and parallel lines, put your knowledge to the test. Solve problems, draw shapes, and explore the world of geometry with confidence.
Conclusion: Your Path to Geometry Mastery
Mastering angles and parallel lines is like unlocking a hidden treasure chest of mathematical understanding. These skills are not only academically valuable but also have practical applications in numerous fields. Embrace the world of geometry, and you’ll find yourself looking at the world from a different perspective.
FAQs
Q1: What are some real-life applications of angles and parallel lines?
Angles and parallel lines are used in architecture, engineering, art, and even navigation. Architects use them to design buildings, engineers for constructing roads, and artists to create perspective in art.
Q2: Why are right angles significant?
Right angles are crucial because they form the basis of perpendicular lines, which are fundamental in creating geometric shapes and ensuring stability in structures.
Q3: How can I remember the different angle types?
A helpful mnemonic is “All Students Take Calculus,” which stands for Acute, Straight, and Right angles, as well as Obtuse angles.
Q4: Can you provide an example of consecutive interior angles?
Imagine two parallel lines intersected by a transversal. The angles on the same side of the transversal and inside the parallel lines are consecutive interior angles.
Q5: Where can I find additional resources for learning about angles and parallel lines?
You can find online tutorials, textbooks, and educational websites that offer interactive lessons and exercises to enhance your understanding of these concepts.